作者:陳愷廷
編輯:黃文滔|量子線上學院特約編輯 (臺灣大學化學系碩士)
審閱:鄭原忠 |臺灣大學化學系教授
1. 前言
學過量子力學的同學,一定聽過海森堡(Werner Heisenberg, 1901-1976)於1927年提出的測不準原理(the uncertainty principle,或稱不確定性原理)。相信大家對測不準原理的理解大概是 — 若想得知一個物體的確切位置,則會因為在測量過程中的行為,使物體的速度失準,反之亦然。但我們應該換個角度看,其實測不準原理和「測量」並沒有關係,而是一個單純由物質的「波粒二象性」所導致的必然結果。
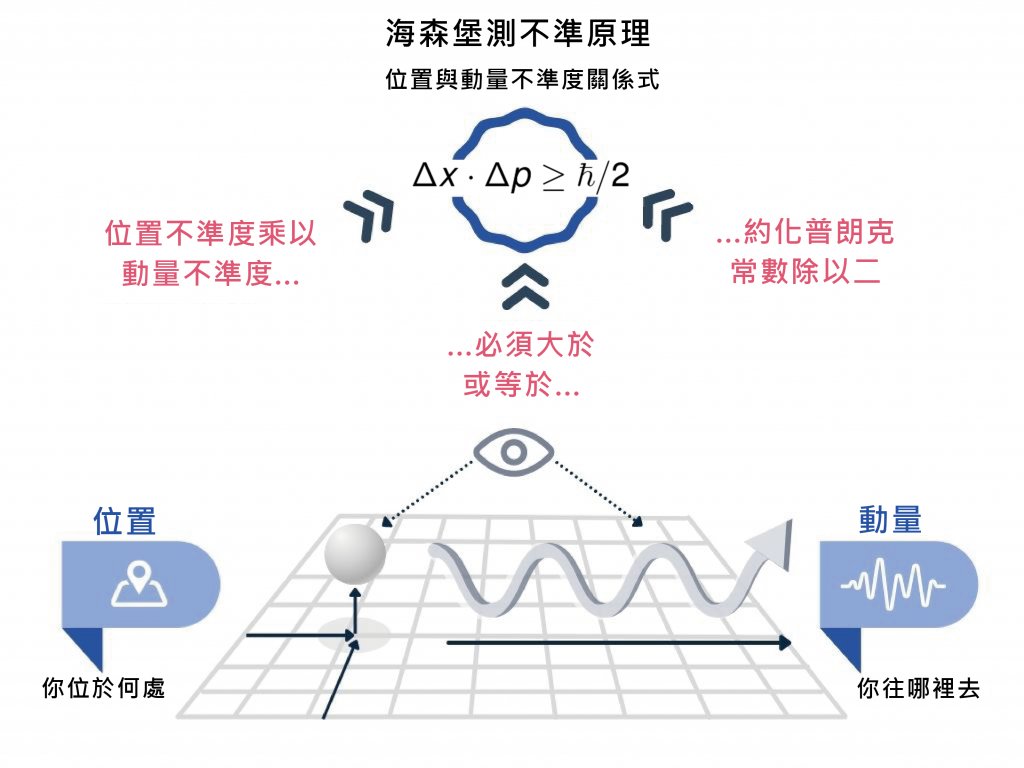
測不準原理描述了物體的位置與動量具有不確定性,並且存在一個最小極限,使得無法同時準確描述物體的位置與動量。這是由於物質具有波粒二象性,其位置與動量的不確定性分別反映了物質的粒子性與波動性。當物質的粒子性較明顯時,其在空間中會具有較確定的位置;當物質的波動性較明顯時,其動量的確定性會較高。
2. 波粒二象性
對於粒子而言,我們可以確定其在某個特定時間下會存在於某個特定位置,然而波卻無法有一個固定於一個點的位置,因為波的形成一定有賴於空間上許多點之間具有同調性的運動。由於波具有這種非定域(delocalized)的特性,我們必須以波函數來描述之,也就是把波在空間上每一點的振幅描述出來。與其說物質一定具有波和粒子兩種性質,不如說粒子就是波,或者說粒子只是波的一種比較定域(localized)的特例。根據德布羅意 (Louis de Broglie, 1892-1987) 的物質波(matter wave)理論,一個物體的物質波是一種機率波,其波長λ由式1所描述:
其中 ℎ 是普朗克常數 (約6.626 X 10 -34) 𝑱‧𝑠,而 𝒑 則代表物體的動量(momentum,等於物體的質量與速度的乘積)。當物體的質量很大或速度很快時,物質波波長就短到無法測量,故於巨觀世界的日常生活中難以觀察到物體的波動性;但若物體的質量很小,如電子等微觀世界的粒子,物質波波長就足以被測得,故粒子的波動性於微觀世界中才能顯而易見,如電子的干涉和繞射條紋等實驗。
3. 測不準原理
了解了波粒二象性,現在要來談談測不準原理。假設有一個純粹的波,我們可以藉由波長求得動量,但無法確定它的位置,那我們該如何創造出一個同時是波又具有粒子性的狀態,從而增加其在位置上的確定性呢?答案是靠波的疊加(superposition)。透過波的疊加,我們可以將原來非定域的波變得在空間上比較集中(或者說更像粒子般在空間中有確定的位置)。 如圖2所示,透過數個不同波長的正弦波(藍色曲線)疊加,可以得到一個在空間中比較定域的波形(紅色曲線)。這是因為波與波之間會互相干涉,靠近中心部分的波因為相位一致(見虛線位置),波會互相加成讓振幅增加,而遠離中心的波相位漸趨不同,因此這部分的波會互相抵消,總體而言便產生比較定域的效果,這樣由多個波疊加得到的局域波型,被稱作一個「波包」。由於疊加的特性,波的位置和動量的確定性並不能夠同時增加。由於式1告訴我們,不同波長的波具有不同的動量,因此當波的動量不確定性越大,表示可以疊加的波可以有更多不同的波長,讓更多不同的波疊加在一起,可以產生在空間上的分佈越狹小的波包,表示位置的不確定性減少了,因此當動量不確定性增加,則位置的不確定性可以減少,相反的,若減少波的動量不確定性,使得可以疊加的波數量降低,就無法得到位置準確的波包了。
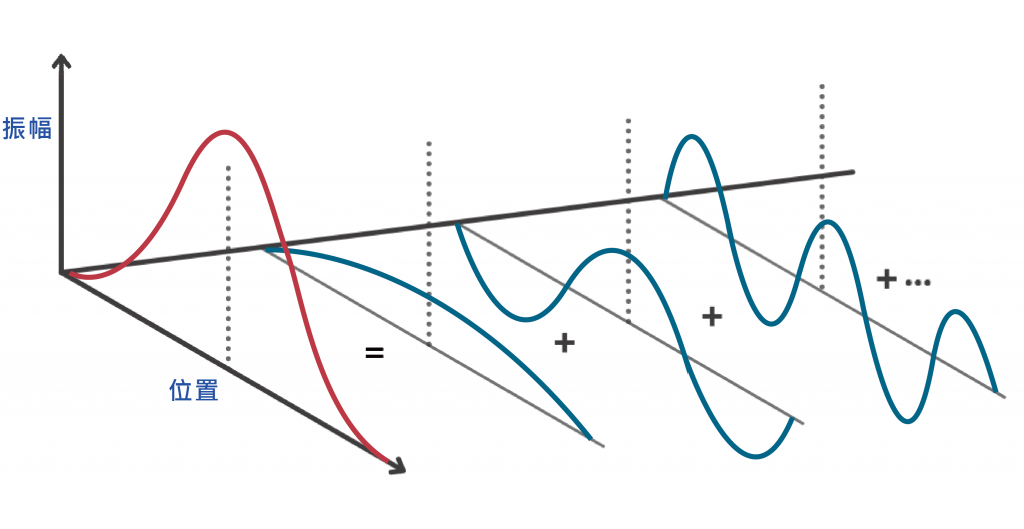
由於不同波長的波之間可以互相加成或抵消,使得各個非定域的正弦波在疊加後可以產生在空間中集中於某個位置的波形。然而疊加後的波形雖然具有比較確定的位置,但相對於有準確動量的正弦波,其動量會變得不確定。
從以上的敘述,我們可以歸納出一個結論—無論如何,都不可能同時精準地得到一個粒子的位置和動量。海森堡在一番推理和計算後,得到了最終結論:
Δ𝑥 ‧ Δ𝑝 ≥ ℎ / 4π 式2
其中 Δ𝑥和 Δ𝑝 分別是位置和動量的標準差,由於兩者的乘積存在一個下限,使得它們不能同時變小 ,這就是海森堡的測不準原理。簡而言之,測不準原理的產生,一切源於「波」的一種先天特質,彰顯了量子力學的波動特性,與測量的方式或者實驗的誤差是沒有關聯的。






