施麗釵 ｜量子線上學院特約編輯 (臺灣大學化學系)
一、前言
「圈圈叉叉」或是井字遊戲我們從幼年時就非常熟悉的，規則很簡單，若是能在九宮格上橫向、縱向或斜向的三個格子內畫下相同字母成功連線就代表贏了。遊戲過程中，我們在格子內填入的圈圈或叉叉是絕對的，並不會因為後續自己或是對手的行為而產生改變。然而，若我們將「量子特性」加入井字遊戲的話會變成如何呢？
二、背景
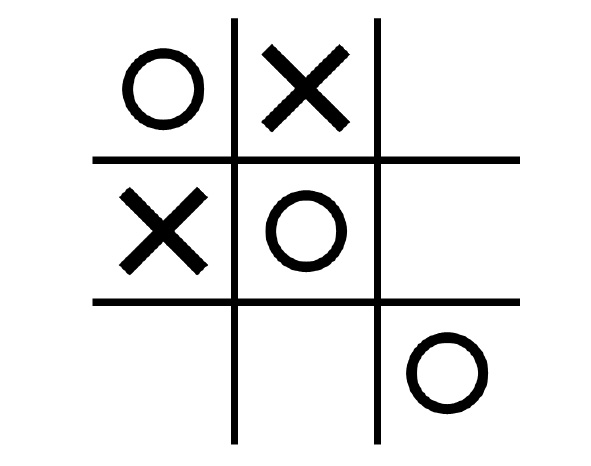
在古典力學中 ，我們可以用精確的描述一個物體位置。而在量子力學裡，物體可能以不同機率處在不同的位置，進行「觀測」之前，我們無法實際確定物體的位置。把量子的性質，包含了「量子疊加」與「量子糾纏」，加入了一般的井字遊戲規則中後，就形成了「量子井字遊戲」！
三、 基礎規則：
玩家每次可以下一對字母在不同格子(也代表格子與格子之間有量子糾纏)，字母在被「觀測」之前都是沒有確定的，也就是格子處在「量子疊加」的狀態，被觀測的字母其量子狀態會「塌縮」(即格子反白)，格子內的字母會被確定。字母被確定後，判定規則同普通的井字遊戲即有三個可以連線的字母就贏了。
那我們甚麼時候需要進行「觀測」呢？當量子糾纏的格子形成了「封閉迴圈」(即格子反白)，則格子需要被「觀測」來決定各個糾纏格子的實際字母。相較於古典的井字遊戲，量子井字遊戲你需要同時考慮到：「對手下的位置是否會在後續進行時影響你的字母？」、「在形成迴圈時要選擇觀測哪一個字母才是最好的結果？」、「是否要主動造成封閉迴圈使觀測發生？」 …等等，有更多需要考慮的層面，歡迎大家去實際一邊玩一邊理解！
如果對前面說明還有不懂的地方，讓我們來看實際例子吧！
四、 實際舉例：
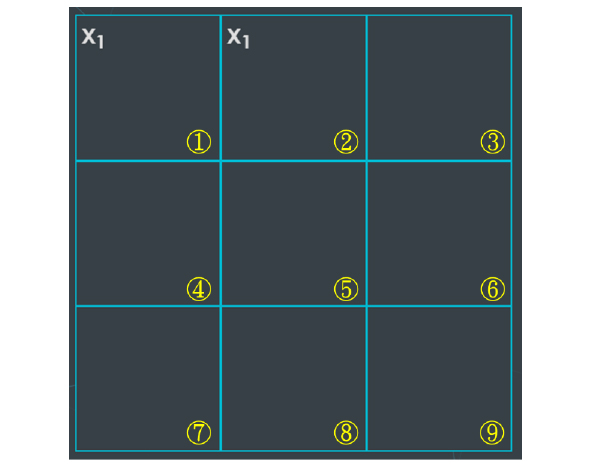
1. 量子糾纏的字母
每次玩家一次可以選擇兩個格子放置一對字母，字母右下角的數字代表回合。在被「觀測」之前，該對字母可以同時存在兩個格子內，且被放置的兩個格子會產生「量子糾纏 」。如果格子內有字母則代表處在「量子疊加」的狀態。
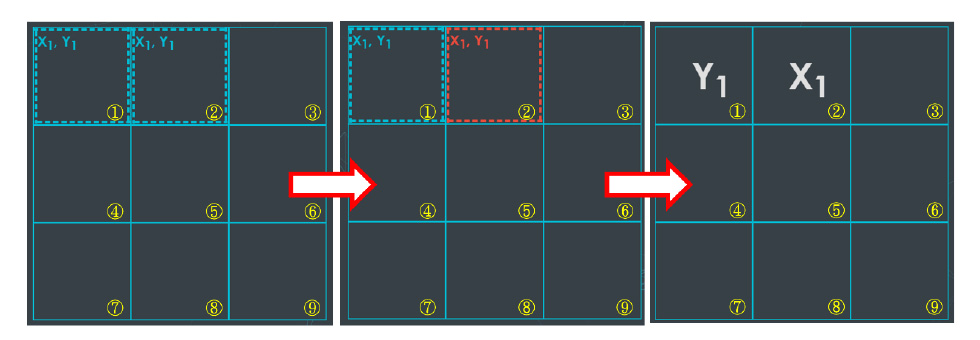
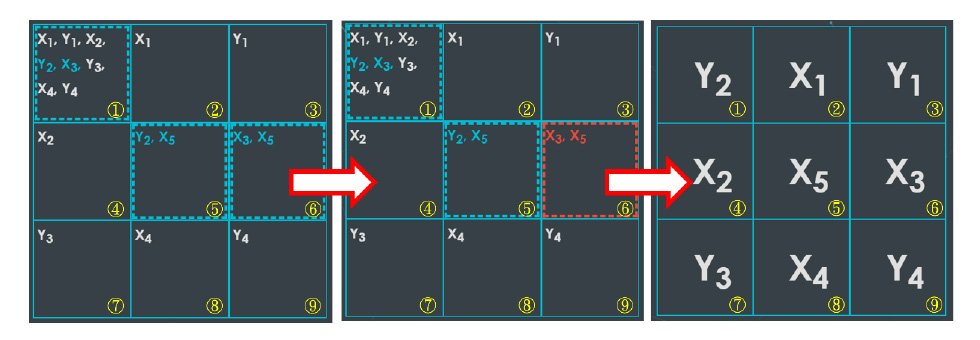
2. 「觀測」形成「封閉迴圈」的格子
*何謂形成「封閉迴圈」的格子：
以一個字母為起點，去觀察另一個量子糾纏的字母(另一半)在的格子中，是否有其他字母的另一半能重新回到起點的格子。
例如(以圖二為例)：
觀察Y1在①格子→另一個Y1在②格子→②格子中有X1→另一個X1在①格子
當互相糾纏的格子由於字母們形成迴圈時，必須從糾纏格子們中選一個進行測量，被選擇的格子會變成紅色，玩家必須從被測量的格子內的字母中選一個進行「觀測」，如此一來，其他同樣處在量子糾纏的格子會進行「塌縮」，也就是其他格子的字母同時也會被決定 。(如圖二與三)
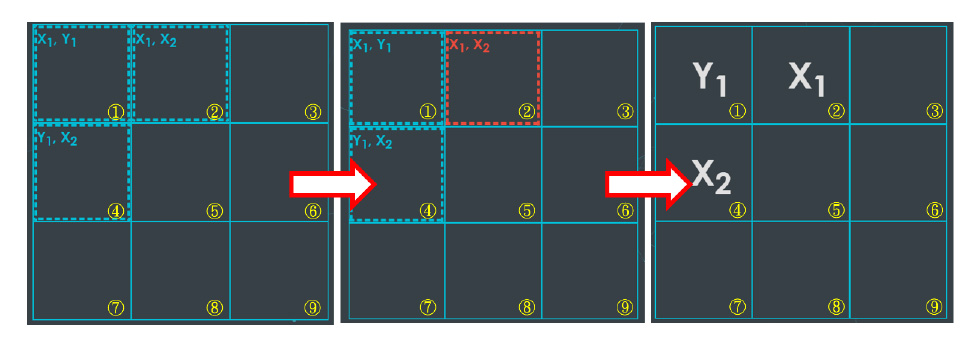
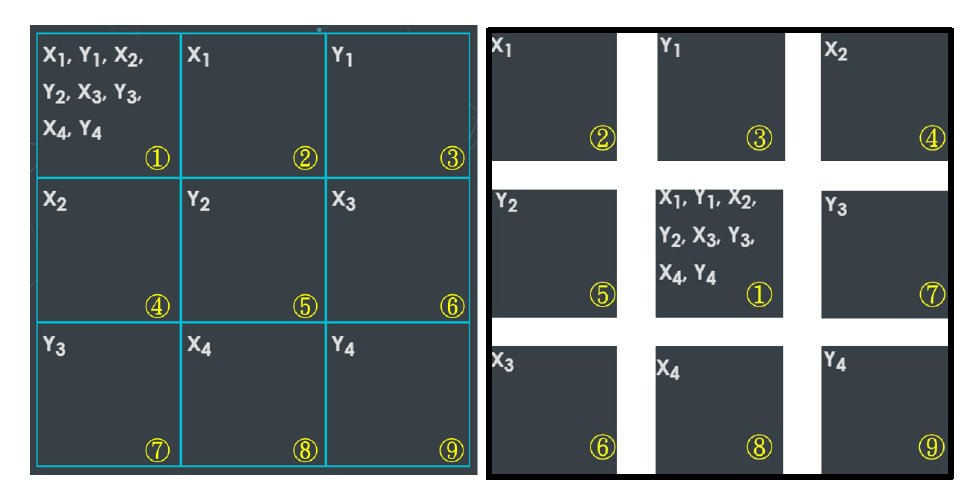
3. 最多「量子 糾纏 」狀態的格子
由於規則是規定玩家每次必須下在不同的兩個格子，若使每次兩方玩家都選中特定格子 ，則最多會出現九個格子互相糾纏的情形(如圖四)。下一次的玩家下的字母必定會造成「封閉迴圈」而需要進行「觀測」(如圖五)。
若是我們重新排列格子便可以輕易發現「封閉迴圈」並沒有形成，因此無須進行「觀測」 。
4. 同時達成勝利條件的判定方式
若是在進行「觀測」完後，雙方同時完成判定勝利的條件，則比較雙方連線裡擁有最大下標的字母，擁有相對較小下標的字母方獲勝，也就是代表在「塌縮」時對方先完成連線。 (如圖六與圖七)
五、 條列式規則：
- 玩家每次要下一對「量子糾纏」的字母在不同格子(代表格子之間有量子糾纏 )
- 字母在被「觀測」之前都是沒有確定的(格子處在量子疊加的狀態 )
- 當「量子糾纏」的格子形成了封閉迴圈，則需要被「觀測」
- 被觀測之後的字母量子狀態會「塌縮」，其他量子糾纏格子內的字母也被確定
- 字母被確定後，則後續判定如同井字遊戲，最先有三個可連線字母就贏了
- 若是雙方同時達成勝利條件，則連線字母中最大下標數字相對較小的一方獲勝
六、遊戲APP：
七、參考資料
[1] Quantum tic-tac-toe – Wikipedia
https://en.wikipedia.org/wiki/Quantum_tic-tac-toe
[2] Quantum tic-tac-toe遊戲說明書 (英文)
https://mathwithbaddrawings.com/wp-content/uploads/2020/10/Game-19-Quantum-Tic-Tac-Toe.pdf
[3] Quantum tic-tac-toe遊戲解說影片 (英文)
https://youtu.be/ZL_kZAEuWSM?si=ApcEM_UWiftl6tZ0
